Intervals

Intervals The Space Between Notes

Suppose we are looking at a piece of music. How does one pick a way to analyze it? If you write out all the notes you will find it hard to understand because each song has different notes, so finding clear patterns will be hard. However, if we instead look at the distance between notes many more patterns emerge. This single idea has spawned much of western theory.

We are good at hearing between notes. This is because while one song may have the notes C to E and another has D to F#, it turns out they are both 4 half steps! This gives up a way of characterizing music that doesn’t care about the specific notes! It’s kind of funny that way. The key takeaway is intervals are a major key to understanding a lot of music and an

is simply a music distance between two notes.

Harmonic and Melodic Intervals

There are two types of intervals. They are harmonic and melodic.

are when notes are stacked upon each other. Meaning the notes sound at the same time. Chords played on a piano for example. Instruments such as Clarinet can only play one note at a time so they cannot make harmonic intervals by themselves. Instead you would need at least 2 clarinets to play at the same time to create harmonic intervals, vs instruments like piano or guitar that can play many notes at the same time and therefore can play harmonic intervals.

are when notes are next to each other in time. They sound one after the other.

Intervals Names

So the name of the game now is identifying and constructing intervals. Creating an interval has two parts:

1. A number

2. A quality

Interval Number

Numbering intervals is easy. Intervals start at the number 1. You can think of it as the note “is itself”. Then you move 1 line or space at a time as you advance to the next note increasing the number for each time you move. Once you get to the next note you have the interval number!

Note that doing it this way means the number is dependent on the staff. Many students get some questions wrong because they look at the notes instead of the staff for the number and this sometimes leads to wrong answers. The staff creates a framework that will be very helpful as we go further, just be careful going forward!

Example 1

Here we have two notes, a D and a G. Starting at the D we have 1, the next line up gives us 2, then a space which gives us 3, and finally we reach the last line that the G sits on giving us 4. Therefore the number is 4. Easy right? Note we could go from the G to the D and this would still give us 4.

Example 2

Consider the notes E to another E. Pick one to start at. Then count each line and space to the other and you will see it comes out to 8.

The number system can go beyond an octave to things like 12, 15, etc… However we are going to focus on the intervals within the octave. For your reference the system repeats itself after 8 (the octave). With 8 acting like the new 1. So a 3 is the same thing as a 10 an octave higher, the only difference is a 10 is an octave higher.

Interval Quality

Intervals have a quality in addition to their number, this is where the notes themselves begin to matter and where things like if a sharp or flat is used can determine the name of the interval.

There are 5 qualities

1. Major
2. Minor
3. Augmented
4. Diminished
5. Perfect

The quality is determined by the number of half steps and the note that is written. There are many approaches to teaching about when to use each quality. I am going to take the approach of a chart to get you started.

Counting Semitones (Half Steps)

Counting how many semitones there are between notes is critical. Let's look at an example:

Here we have the notes C and E. There are two tools I recommend for counting half steps. First a piano or other tool that physically shows notes. Second a chromatic scale. I will use a piano in my explanations since it is the same going up and down.

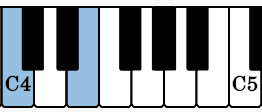
We start at the note C. We have not yet moved so the semitone count is 0. Now we go to the next note, C#. We have moved a half step so the semitone count is 1. We continue to do so until we reach E. In order we have C (0 ST) -> C# (1 ST) -> D (2 ST) -> D# (3 ST) -> E (4 ST) where ST stands for Semitone. We see the number of semitones is 4.

So all you need to do is find the note on a chromatic scale, piano, or other instrument, then simply count to where the ending note is! Just remember we start at 0 since we have not moved any semitones at the first note! This can often be confused with the interval number which starts its counting at 1 because the first note is unison or a P1.

---

Double click or (ctrl + click) to reset / Mouse wheel to zoom to mouse location / Click + drag to pan view

---

Close

Common Intervals

Before we move on to the more general case of all intervals let's just consider the simple case of intervals on the chart. These intervals are very common so they are worth learning first. Once you can use the chart comfortably it will then be easier to expand out to the broader system used to identify intervals.

Here are the steps to solve simple intervals:

Interval Naming Steps

1. Get the interval number (Recall counting starts at 1)

2. Count how many half steps it takes to reach the other note. (Counting starts at 0 since the first note has not moved any half steps)

3. Look on the chart for the interval number that matches in the name and that also matches the number of semitones. It must be that interval.

Example:

From example one we had:

We identified the number as 4, and if you count the semitones you will find it is 5. Looking at the chart in the interval names we see there is only one name with a 4 in it and it does have 5 half steps! Therefore the interval must be a Perfect Fourth, or P4!

For this quiz use min for minor, maj for major, aug for agumented, dim for diminished and p for perfect. Do not use a space. For example major second is maj2, minor third and min3, perfect first is p1.

Tritone is not accepted, use aug4 or dim5 accordingly.

Interval Construction

---

Double click or (ctrl + click) to reset / Mouse wheel to zoom to mouse location / Click + drag to pan view

---

Close

Reveal Answer