Goal
Understand sound reflections and how to calculate where they will go.
Possible Sound Movements
Unless you’re in a free field, or in a perfectly absorptive environment sound will attempt to come back to you by reflecting off surfaces. In fact, three principle things happen.
Sound reflects off surfaces and so stays in the room.
Sound transmits through a surface and leaves the room.
Sound is absorbed by the surface and transformed into another form of energy, typically heat.
There is a fourth property when you include a human, and that is that reflections create an auditory “image” of where a sound localizes from.
A reflection is when a wavefront bounces off a surface sending it in a new direction. In acoustics when we talk about reflections, we do so in the context of a specific sound wave coming back to a point, which is usually our listening or micing position. This is typically shown as a “ray” of sound.
A sound source however emits a wavefront, which is a set of points in space effected by some event which in this case is a pressure wave.
Talking about entire sets of points as a wavefront is often hard to do and so it’s typical to talk about results at points as it’s easier and often just more practical.
Lifecycle of a wave
When a wave reflects off a surface several things happen. Say I have a speaker emitting a tone in a room that has acoustic panels on the walls. First the wavefront travels through the air and loses some of its energy by friction through the air. Then the wavefront hits the panel absorber as an incident wave. Depending on the absorber’s density and material some of the sound will enter the absorber and get turned into heat. Some sound will reflect off the absorber and bounce back into the room. Some sound will also transmit right through the absorber and then encounter the wall where the process is repeated. Since the absorber is denser than air the sound will also refract and speed up in that medium and all these events happens again when it gets through the absorber and hits the wall since the wall is denser yet! All the while losing energy. Note that every reflected wave will always be weaker than the incident wave.

I know I just threw the kitchen sink at you, but it helps to see the complex process you're dealing with. Geometry will come into play as both shape and size can play significant or negligent rolls depending on the frequency. Properties of material and sound also play a big roll and despite the many theories we have, much of the process of treating a room is still recording room responses and adjusting based on the data we get back, guided by principles of course.
Three Types of reflection
There are three primary ways we talk about reflections.
Early reflections
Late reflections
Diffusion
When someone refers to reflections, they are nearly always referring to specific parts of a wavefront. While this isn’t always the case it is often enough that it’s implied most of the time. These are early or late reflections and are generally addressed because they are a problematic part of a wavefront, which is another reason why reflections are typically shown as rays. A reflection in one part of the room may not be a problem but another reflection in another part of the room may be a big problem! Diffusion can refer to the entire wavefront, a larger portion of the wavefront, or a small part, but it is always referring to those reflections getting spread out to the entire space. Diffusion will be covered separately.
You can reduce unwanted reflections by placing absorbers up that turn the acoustic (sound) energy into thermal (heat) energy, but all rooms except for ones that are heavily treated will have some noticeable reflection off objects and walls nearby.
Each surface sound can reflect off will also have some frequencies it may absorb and transmit. For each time a reflection bounces off a surface before coming back to the point in question we count it. The number of reflections is called the order of the reflection. For example, if a sound bounces off 1 surface before coming back then it’s a first order reflection. If it bounces off of 2 surfaces, then it’s a second order reflection. These reflections are often also early reflections, which are reflections that occur below the echo threshold, typically below 20ms but can go much higher depending on content. These are significant because they occur so fast that we generally perceive them as part of the direct sound. This means they have a direct bearing on the sound’s initial characteristics and are the first focus of most acoustic treatments. Small order reflections should also be considered as these will directly influence certain frequencies causing decisions such as how close to place a mic to a sound source or to a wall to matter more than it would normally if such a reflection did not exist. Any reflections of a high order usually don’t matter nearly as much because the wavefront loses much of its energy after many reflections.
Some wavefronts, and by extension frequencies, may get boosted or cut dramatically depending on the room and its set up. For example, if a bass player is jamming out in an untreated room and finds that the note F2 is softer than normal in the recording then there could acoustic problems causing this to be the case. Such problems may be resolved by adjusting the mic by only an inch, or even less and could have a big impact on this. It's these types of situations we wish to avoid.
Properties of Sound Reflections
Different frequencies will reflect by different amounts depending on material.
As long as the medium is the same the speed of propagation will remain the same.
The direction a sound is reflected depends on the geometry of the surface and potentially its refraction (refraction will not be a factor most of the time).
Let's briefly discuss each property.
Reflection off Different Materials at Different Frequencies
Different frequencies reflect by different amounts depending on material. That is because each material will absorb sound, meaning it will turn the sound energy into thermal energy. Each material will also allow some sound to transmit through the material to some degree. The dimensions of a material will also have an impact on how much reflection takes place.
We nearly always use absorption coefficients to describe how much sound is absorbed by a particular material instead of talking about how much is reflected. Absorption coefficients are used because they help solve problems with sound reflecting back and so make more sense to use from a problem-solving perspective. It’s also easier to measure them. Often, we consider 100% of the sound to be reflected and any sound not reflected then must have been absorbed, and although the real world is not like this because sound can transmit through an object, it often yields useful insights into how a particular room should be set up. Because if the sound doesn't come back then in a sense it's totally absorbed.
Here is a basic table, but before you use it you should know it is very general. It is a table I was given when I took acoustics. When designing you should always look up the acoustic properties of the given material. This is just a good general table for rough approximations.
| Type of Material | 125 Hz | 250 Hz | 500 Hz | 1000 Hz | 2000 Hz | 4000 Hz |
|---|---|---|---|---|---|---|
| Brick | .03 | .03 | .03 | .04 | .05 | .07 |
| Carpet (Heavy, on concrete) | .02 | .06 | .14 | .37 | .60 | .65 |
| Carpet (Latex, on foam rubber) | .03 | .04 | .11 | .17 | .24 | .35 |
| Concrete | .01 | .01 | .015 | .02 | .02 | .02 |
| Wood | .15 | .11 | .10 | .07 | .06 | .07 |
| Glass (Large heavy plate) | .18 | .06 | .04 | .03 | .02 | .02 |
| Glass (Ordinary Window) | .35 | .25 | .18 | .12 | .07 | .04 |
| Gypsum Board ("Drywall") | .013 | .015 | .02 | .03 | .04 | .05 |
| Plywood | .28 | .22 | .17 | .09 | .10 | .11 |
| Audience (On upholstered seats) | .08 | .27 | .39 | .34 | .48 | .63 |
| Concrete Block | .36 | .44 | .31 | .29 | .39 | .25 |
| Light Velour (Fabric on wall) | .29 | .10 | .05 | .04 | .07 | .09 |
| Plaster | .44 | .54 | .60 | .62 | .58 | .50 |
| Wooden Pews | .57 | .61 | .75 | .86 | .91 | .86 |
| Chairs (Unoccupied seats) | .15 | .19 | .22 | .39 | .38 | .30 |
Many tables like this can be easily found. Often it is desirable to know the thickness of the material which is often not listed so some research may be needed in order to get the needed info. We will visit absorption as a topic later.
If the Medium is the same the Speed of Propagation will stay the same
There are 2 major factors to consider when talking about reflections that can change a sound. They are density and temperature. Ideally a room will be homogenous, meaning it is the same throughout, so that no significant changes happen to frequency content. If there are such changes the reflections may be altered, sometimes noticeably. When density changes the speed changes and this can throw off calculations for where to place speakers, calculating interference and other such tasks. When such effects happen, we call it Refraction and will talk about it more in that section.
The Direction a Sound Reflects Depends on the Geometry
When you sit in a room and hear something, you hear not only the direct sound, but also sound that had to bounce off one, two or more surfaces to reach you. Each surface causing the sound to be changed is some way. These changes in the reflected sound tell you things about the room. If the delays take a long time, then you know you’re probably in a big room. If there is a lot of high frequencies in the room then you know it may be made of tile, brick, wood or some other reflective substance. If you hear a lack of these things, then the room may be carpeted or have been treated to sound a specific way. You take in incredible amounts of information all from simply hearing a “room”. In fact, room tone is just a recording of the room when nothing is going on. It's literally just the room and is a must have recording for serious ADR (Automated Dialog Replacement) done in the movie or television industry today.
Sound gives us such information because it moves in very predictable ways. Namely that when a sound hits a wall its angle of incidence will equal its angle of reflection.
This is great because this is also how light behaves. This means if you want to know which sound reflections are going to hit you first from the walls you can find out by simply having someone sit in the listening position. Then have another person take a mirror and move it along the wall you want to measure. When the person in the listening position can see the speaker cone in the mirror then you have found a spot in the room that will reflect back to the listener and hence that distance and the frequency its related to should be treated. There will be an early reflection point on the wall for each speaker you have. This process will only reveal first order reflections. You will need math to find the higher order reflections.
These early reflections can also misinform our judgment. For example if you are listening to 100 Hz in a room with no treatment and lets say this room also has some nasty first order reflections, then you will hear the direct sound from your speakers and the first order reflections in your room which will combine with the direct sound after a delay. If that delay is under 20ms then your brain will interpret it as direct sound and now you have a false idea about how loud 100 Hz is! Not only this, but your ability to tell where the 100 Hz is in space will also lack because both the intensity cues and time cues have been manipulated. This is referred to as the Hass effect. For this reason, we don’t want reflections of this nature and seek to treat them.
Some set-ups can have a particularly hard time with early reflections, such as setting speakers up in the corner of a room. This particular situation can be extra bad because second order reflections can also have a major impact. For rectangular rooms it is better to place your self facing the longer side than the shorter side. Sound that is meant to come out both speakers and hence sound "centered" is much more of a concern than that coming from the sides. Therefore we should optimize these angles first which are the ones that lie directly behind us. This is one reason why using the longer length of the room is recommended.
The goal is to set up a “flat” room where no frequencies are manipulated in a way that greatly effects your judgment of them. Say you do this mirror trick and you find several places in the room that this first reflection occurs at. They can happen on the ceiling, the walls, the floors, and on objects. The major problems are large flat surfaces and most objects often are too small to matter or act more like diffusion. So, focusing on the problems resulting from the walls you find several distances that can be trouble. Say the distances of 15 feet and 24 feet are among those that a measured from your listening position to the wall.
To address this, you need to find the fundamental frequency that these distances correspond to. Then you need to consider those frequencies and their integer multiples. As the frequencies get higher it will be less of a problem, but for the first few multiples and their surrounding frequencies this can be a problem. Using the formula f = (1/T)1130 ft/sec we obtain 75 Hz for 15 ft and 47 Hz for 24 feet. So, if we want to treat the problem caused by these reflections, we should place absorbers at those locations which are made to absorb 75 Hz and 47 Hz. Higher frequencies in the harmonic series of the respective fundamentals will also be diminished by those absorbers, or we could alternatively place diffusors that cause the reflection to be spread out more. We will get into both solutions in their respective sections. For now, understanding how to locate these first order location spots and determine the frequency range that must be treated is our aim. We now know using the mirror method how to do so.
Standing waves are another area that can be treated in a similar fashion and we will see that because we understand how angles work, we can compute the problem frequencies of a room given we know the shape of the room. Luckily there are room calculators for such a job. Troldtekt is such a calculator. You can give it some simple shapes of rooms and tell it the material properties it is made out of and it can compute for you reverb time for each frequency (a topic we will get to in RT60) and it can also show frequencies that will be effected by the shape of your room just based on its geometry and give some insight on to the type of absorption your room may require. Another great site is amcoustics.com which also gives you much greater insight to the room modes (we will cover this in the modal resonance section) and the most problematic frequencies. Interpreting the results will come in a later chapter because we are still building up the basics.
I want to briefly mention that some materials are made to take advantage of refraction to change the angle of refraction. We will go over refraction more later but in essence when a wavefront enters a medium that changes density it will change speed and direction. We can leverage this to spread a wave out. We will not focus on such technologies but I want to at least mention them.
Types of Reflections
There are additional types of reflections that are not designated by their timing, but rather their direction. Additionally there are some special cases that you are very likely to run into many times. These are flutter echo, specular reflections and diffuse reflections.
Specular and diffuse reflections
Specular and diffuse reflections can be imagined as the way light bounces off a mirror. You can shine light onto a mirror, and it will form an image, a very clear image that directly reflects the subject. If you look in a mirror you see yourself. This is because the wavefront of photons bouncing off you and onto the mirror bounce in the same direction. This is a specular reflection.

On other hand a diffuse reflection is a like you looking at a wall. Light bounces off you and reflects off the wall, yet no image of you is formed. This is because light that bounces off you and onto the wall bounces in multiple different directions. When this happens, we call it a diffuse reflection.
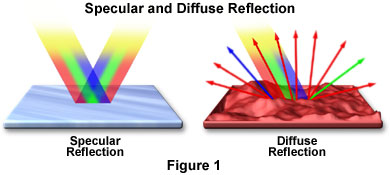
Similarly, in sound when a discrete echo happens, such as you yelling “HELLO” into a canyon and hearing “hello” echo back you are hearing a specular reflection. A diffuse reflection is more like you yelling “HELLO” in a large echoey room where you cannot tell where the sound initially came from or even what the word is. When we talk about treating a room, we use these two types of reflections. Some studios such as Sun Studio made famous the “slap back” echo which can be achieved acoustically by specular reflections off of walls.
Incident Wave directional properties
We call something normal if it is at a right angle. This property is extremely important and will come up over and over because diffusion, absorption and reflection all depend on the angle of incidence. Normal reflections have special properties, especially if it’s a specular reflection. For example, a ball bounced directly above a table bounces straight up, its bounce is normal to the table. In fact you can think of how a ball would bounce and in most cases it will match with what sound would do.
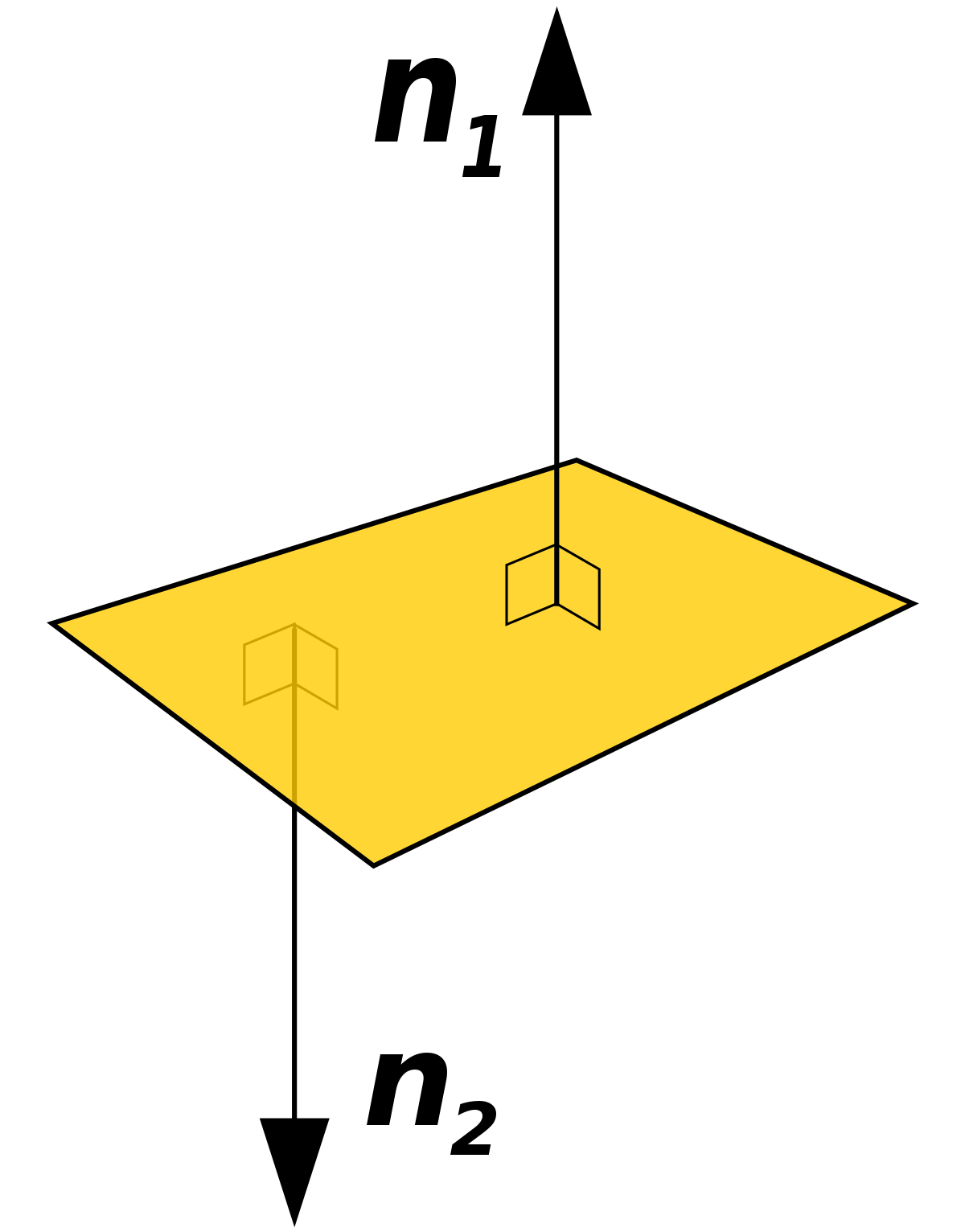

In particular if an incident wave is normal to a surface its reflection has the potential to cause pressure to double as the reflection collides with the incident wave. Remember sound waves are just pressure variation and this property of doubling when its normal will become a serious problem when dealing with specular reflections.
Standing Waves
We will get into standing waves in much more detail later when it comes to acoustic treatment but knowing the basics of them now can be very useful.
Standing waves are the result of reflections that reinforce each other to create consistent nodes and anti-nodes. A node is a 0 point on a wave, while an antinode is a maximum or minimum on a wave.
Standing waves result when the distance between two parallel surfaces matches the wavelength of some frequency. When the room is excited some of the wavefront will hit one of the walls. Some of the reflected sound will be normal to that wall and send a reflection to the parallel wall which will send another normal reflection back. Since the wavelength will fit neatly between the walls the wave will sum constructively and you will wind up with a frequency that lasts much longer than usual. This is called a resonant frequency. Not only this but since the wave fits snugly between the walls the nodes and antinodes don’t move! This causes “dead spots” for that frequency in the room as well as spots that are much louder than it should be. Since they don’t move, we call it a “standing wave”. Standing waves begin a long line of curious problems. You can try this out for yourself in your room. Just play a low bass tone, say a sine wave of 40 Hz loudly over your speakers. Then get up and walk around and you will find some spots of the room appear to have no sound at all while others are much louder! Can you image mixing or recording with such issues?
Pipes have standing waves built in, your ear canals, flutes, clarinets and many other musical instruments take advantage of it, but unfortunately rooms do to.
Additional Geometries
Convex
When a planar wavefront hits a reflective convex surface, the wave spreads out in all directions. This is very useful for diffusion. The size of the wave must be large or comparable to the wavelength it’s meant to effect. This is true in general.
Concave
Concave surfaces when reflecting a wavefront will be focused to a point. You can imagine the acoustic properties that buildings with dome structures will have.

Corner Reflections
Corner Reflections send a sound back to its source.
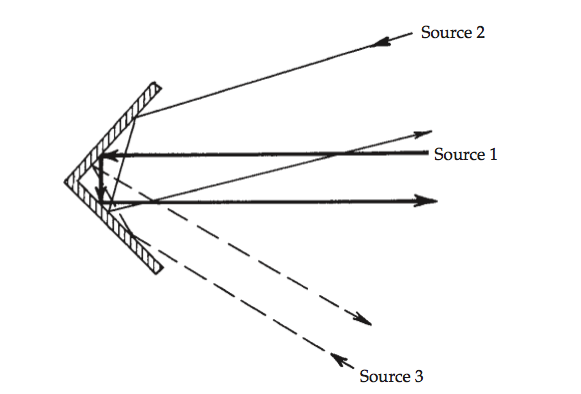
So you can see why adjusting these positions can have good effects acoustically. This is also another reason why setting up in a corner is a terrible idea.
Additional Patterns
There are many other types of reflectors I may get to in later iterations of the book, but this will work for now. A special case I will only mention for you to look up if you want to know more is the case of a parabolic reflector. These have some interesting sound properties for creating parallel sound fields.

Whispering Galleries
If we combine concave parabolic reflectors just right we can create a room that collects sound at specific points. There is a whole load of cool stuff here we could talk about but one of these applications is a whispering gallery. These rooms have locations where you can talk and easily hear the person across the room if you are both standing in just the right location. Here is a video demonstrating it:
Flutter Echo
As soon as you go from a single specular echo to multiple specular echoes you being to run into flutter echo. This is a common occurrence in tiled, brick and other reflective rooms with little to no diffusion. If you have ever clapped your hands in a tiled bathroom and listened to the ringing that happens, you’re a listening to “flutter”. Often people turn right to absorption to treat the problem (if you decide it’s a problem) as its usually more of an issue in the higher range of the spectrum and thus often be easily absorbed, but diffusion is another option that can easily break the specular waves up and get rid of the flutter.
Here are some video examples:
The Mean Free Path
It is useful to talk about the average length a reflection must travel in room as a measure of the reverberation in the room. We are assuming that plane waves are randomly traveling in all directions which can be approximated by late reflections. We also assume the absorption coefficient for the materials in the room are all the same, otherwise a more complex version of the equation is needed. This information can inform one on the properties of the reverberation in the room and give estimates to the number of reflections happening. Of course, this calculation is assuming your room is empty, so take the result with a grain of salt!
The average (Mean) distance sound travels between successive reflections. The distance can be found using: MFP = 4V/S Where V is volume and S is surface area.
In a room of 25ft x 20ft x 10ft sound travels about 10.5ft between reflections. This implies it takes 9.3ms for a reflection to travel the mean free path. In other words about 107 reflections take place in about a second.
Example
In the case of a room that is 12x14x8 we get the following:
So, we have an average length of 7.15 ft that reflections travel before they are reflected. Using this result, we can calculate the approximate reverberation of the space. A sound wave takes about 6.6 ms to go 7.15 ft. So, 1/(6.6x10-3)= about 152 reflections a second.
Problem
In a room of 15ft x 25ft x 10ft What is the mean free path? How long does it take sound to travel this distance? Approximately how many reflections a second take place?
To support this series please consider donating via
paypalor joining the
patreon.