Equal Loudness Curves

What is loudness?

Loudness is something that is determined by humans. Notice we do not measure loudness, we measure pressure, or intensity, or something else that can be directly measured. What is loud to one person may be soft to another. For example, you may find a loud 10 kHz tone very annoying but an 80 year old man may barely notice it!

We do have a "loudness unit" now, called LUFS, or Loudness Unit Full Scale. However, how we arrived at such a unit is what we will be more concerned with here. How does one begin to quantify something like "loudness"? Well, Harvey Fletcher and Wilden A. Munson decided to do a simple test.

The idea of a loudness curve

While loudness may be hard to quantify, variation in perceived loudness is easier to measure. Here is the idea, we play a specific reference frequency at a specific SPL. We then play another "test" frequency at that exact same SPL. We then ask the listener if the test frequency should be turned up or down to match the SPL of the reference tone. We then continue to do this until the listener has concluded they are the same loudness. The difference in movement is thus what it take to make that test frequency the same "loudness" as the first.

We can continue to do this for all frequencies at that particular SPL until we have done them all. It will produce a curve known as an "equal loudness" curve because it is how much each frequency must be turned up or down to get that loudness.

Example

To make it a little more concrete suppose we ran this test. We decided to choose a reference frequency of 1 kHz at 40 dB_SPL. For our test subject we play the 1 kHz tone at 40 dB_SPL. We then play 100 Hz at 40 dB_SPL. We then ask them if it should be turned up, left alone, or turned down to match the reference. We receive the answer to turn it up. We do so and continue to ask until they say they are the same. In the end the 100 Hz signal is now at 57.7 dB_SPL. That is to say, if we want 100 Hz to sound sound the same as 1 kHz at 40 dB_SPL we would need to turn it up by 17.7 dB_SPL.

Contour Lines

We can then take this a step further. Say in our first run we used 1 kHz as the reference tone and ran the test at 40 dB_SPL. Now suppose we ran it again for a reference of 50 dB_SPL, and then 60 dB_SPL etc... Each time we would generate an entirely new "equal loudness" line.

These experiments have been repeated, with the most recent standard of ISO (International Organization for Standardization) 226 being done in 2023. Most current charts show the original Fletcher Munson curves (made in 1933) over layed with the 2003 revision. Note that these curves are averages, your specific curve will be different. Also keep in mind that the number of frequencies tested will affect the data as well.

Because we use the more recent measurements for our standards the name "Equal Loudness Contour" is a better fit than "Fletcher Munson Curves" though you will often see the names interchanged freely.

---

---

Close

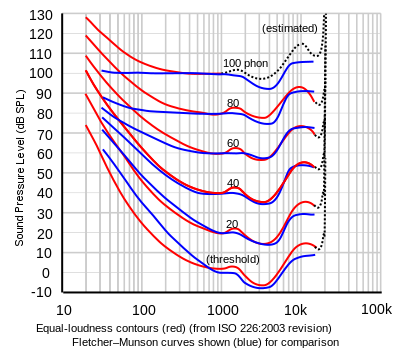
Observations

First note that at low dB_SPL we need to turn up low frequencies a lot, and high frequencies as well. The lower the frequency the more it must be turned up.

Next note that at as dB_SPL increases, the curve tends to flatten out suggesting that higher dB_SPL yields a more "even" representation of the spectrum to us. The resonance of the ear also tends to play less of a role as the dB_SPL increases.

Is it loudness?

While this shows there is a spectral imbalance that appears to be consistent across people, consistent enough to produce these averages, we still have several other factors to consider. The length of a sound, the content of a sound, the amount of spectral change in a sound! These are major factors in loudness not considered here. As such, while the equal loudness contours give us some general hints it is clear they fall short of "loudness" in the broad sense of the word.

For the remainder of this lesson when I use the term "loudness" just know it comes with all of these short comings. It's not true "loudness" but it is much better than just using dB SPL as that is clearly way off if such large adjustments are need to make things sound "equally loud"!

The Phon

It is helpful to move away from the dB SPL when talking about a specific loudness line. For example it is a mouthful to say 100 Hz with the reference of 1 kHz at 40 dB_SPL. So what we do instead is define the reference to be 40 phons. Then every point on that line is understood to be referenced to the reference at 40 dB_SPL.

The phon thus relates the loudness to the dB_SPL, but it gets rid of the need to constantly state the reference. You can say the 40 phon line at 100 Hz or 10 kHz and it is understood that one must use the reference of 1 kHz at 40 dB_SPL. More importantly the change in dB SPL is included in the phon line directly. We don't need to state how much 100 Hz had to change in dB_SPL because we are talking about the specific loudness line. It is understood that you would have to look it up on the graph.

The Sone

An increase of 10 dB_SPL is associated with a perceptual doubling of loudness, as a kind of quick and dirty rule. The problem with this is using dB_SPL for loudness is not a great measurement. A 10 dB_SPL increase at 100Hz is very different than at 1 kHz! However, we have related dB_SPL to loudness through the phon. This does take into account the variation required to keep the loudness equal, hence going up or down by 10 phons is similar to doubling or halving the loudness. We define the reference (1k at 40 phon) to be 1 sone. Then for a 10 phon increase the sone will double, and for a 10 phone decrease the sone will half. This gives the following scale:

So if we describe the loudness in sones a doubling of sones directly relates to a "doubling" of loudness. Its a 10 dB rule but includes the variation in loudness so its good for all frequencies! This scale is for sine waves, there are nuances I am leaving out for more complex signals. I just want you to know what the "sone" scale is.

Questions

1. How does the phon scale differ from dB_SPL?

2. What would the nearest phon rating of a 100 Hz sound that has a decibel rating of 90dB_SPL?

3. How is a sone different than a phon?

4. How many times louder is an 80 phon sound to a 40 phon sound?

5. How many times louder is an 60 phon sound to a 70 phon sound?

6. A sound is measured to have 90dB_SPL at 100 Hz. What is its sone?

7. A sound is measured to have

   $10^{-4}\frac{W}{m^{2}}$
   at 100 Hz. What is its sone?